Game Theory Paper

Nature Goes Last: Extensive Normal Form

Introduction:

I decided to dive into an issue that has been at the forefront of sports in America: The NCAA and payment of players. To give some background, the NCAA brings in roughly $1 Billion each year, and that number continues to grow. Sports such as football and basketball receive national attention from the biggest brands and sponsors. This has made the issue increasingly more controversial, as the NCAA clearly has not paid its athletes properly for their value. However, the reason why this is even more relevant now is the passing of the Fair Pay to Play Act in California. Under this law, players would not receive payment from school, but would be able to accept sponsorships for their likeness and image. More states will be deciding this case over the next couple of years. Players have been punished in the past for taking any money for an advertising or sponsorship, so this would be a way to combat that. I will go through two games of different forms, both relating to the same issue.

Players:

This game consists of two players. Player 1 is the Sponsor, who can either offer the athlete an endorsement or not. Player 2 is the athlete, who either accepts or rejects the offer. Nature is also involved, and acts as the court in this game.

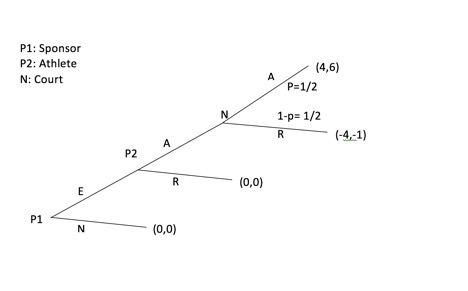
Here we have a sequential game. Player 1, the sponsor starts off the game by either offering an endorsement or not to Player 2, the athlete. If Player 1 does not offer the endorsement, then the game ends, with both players receiving payoffs (0,0). If Player 1 decides to offer an endorsement deal to Player 2, then the game moves to the athlete’s choice, as he/she can either accept or reject the offer. If Player 2 rejects the deal, then the game ends, with both players receiving payoffs (0,0). As you can see, nature is the court, and acts third in this particular game. The court will either accept or reject the proposal to allow the athlete to be paid by the sponsor. If the court accepts the contract, both players receiving a high payoff of (4,6). However, in the case that the court rejects the offer, then the payoffs would be harsh for both players, resulting in (-4,1). The game will end after the court (N) makes its choice. The chance that the court either accepts or rejects the offer is represented by X and 1-X, which both are equal to ½.

Payoffs:

I used the equation (B-E) to solve the payoffs for P1, signifying the benefits of the endorsement subtracted from the cost of the endorsement. This is used for the sponsor, as they are deciding to offer the player an endorsement is 100% a business decision. That being said, it is imperative that the benefit of giving the athlete the endorsement will exceed the payment that is being made to the athlete. B=10 while E=6. For the athlete, their payoff is just the amount of money (E) they receive and not based on any other benefits that come with the endorsement. As you can see, P2 benefits more from the endorsement, as they do not have to pay for the endorsement like P1 does. The payoffs for choosing “N”, and the deal not going through are pretty straightforward, as (0,0) displays that both players are neither better or worse off than they were before. If nature rejects the sponsor from paying the athlete, then they both have negative payoffs as shown by (-4,-1). The sponsor (P1)is worse off because they put more of an investment into the athlete (P2), so they lose money they would have made with the endorsement. The athlete is still worse off than if they rejected the offer in the first place, which would have ended the game. They are now worse off because they were told they were going to be paid before the payment was revoked, resulting in the -1. However, they do not receive as bad of a payoff as Player 11 because they did not have any money in the first place.

Solution: The game can be solved using backward induction. The nash equilibrium comes out to AA (4,6) as this is the best option for both players to play in this game. This is where they receive the best payoff, so it is a pure nash equilibrium.

Game 2: Nature Plays First:

Since I found my original game to be pretty simple and straightforward, I decided to change the order of the game to add some complexity to it. For this game, it is almost a continuation of the previous one, but is in Bayesian extensive form. While the last game looked at the court and whether or not athletes would be allowed to get paid, this game goes into different elements of the game. So, assuming the court decides to pass this law that would allow athletes to be paid for endorsements, what happens next? Do all athletes get paid? Or just a certain type of athlete? Those are the sort of details that this aspect of the game will dive into.

Players:

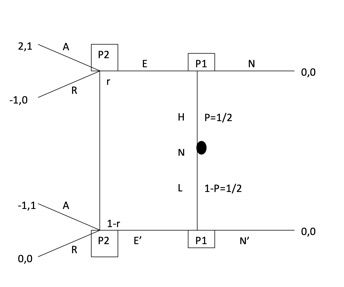
Player 1 is the sponsor, who will decide to offer endorsements to the athlete (EE’) or not (NN’). Player 2 is the athlete, who will either accept or reject the offer. As you can see, nature will go first in this game. Nature determines if the athlete is a “high type” or a “low type”. The chance of the player being an “H” or an “L” is equal, as is demonstrated with X=1⁄2 and 1-X=½. This game is simultaneous and not sequential , as the players will now make their choices not knowing what each other picked.

Payoffs:

The Payoffs are pretty straightforward for this one, as “NN’” will once again result in a payoff of (0,0) with neither player being better or worse off. High type athletes have the opportunity at a higher payoff, getting (2,1) if the Sponsor decides to pay them. For low-types, there is still potential for getting endorsements, but not as high of a payoff for either player in this case. If the low type accepts then he/she will get payoff (1,-1). If the athlete rejects the offer, than player 1 will be worse off if it is a high type athlete, as shown (-1,0). However, they will receive (0,0) if the low type rejects the offer. For low type athletes, the benefits and endorsement amounts are lower, due to the fact that the athlete is not as talented.

Solution:

Separating 1(NE’)

P2 chooses A,

P1 chooses EN’, no PBE

Separating 2 (EN’)

P2 chooses A,

P1 chooses (EN’), so there is a PBE

Pooling 1(EE’)

P2 chooses A,

P1 chooses EN’, so no PBE

Pooling 2 (NN’)

There is PBE for (NN’)

The PBE is present in (EN’) and (NN’). This makes sense for the game, as P2 is actually better off to not offer the endorsement in some cases. There is not one set strategy that always works for Player 1, whereas Player 2 is better off to always accept the offer, whether they are a high type or a low type.

Conclusion:

The lesson of this game was to solve this game in different ways, keying in on different elements of the issue. I really wanted to focus on the story of what is going on, and then found ways to apply it to different forms. Game 1 was a more straightforward court case, as nature had most of the power in deciding if the deal could go through or not. In game 2, nature again has power, as they determine whether the player is a high type or a low type which determines the payoffs. Overall, I feel as though the solutions and payoffs were the most difficult part in determining, which really forced me to think critically. It was very intriguing to apply game theory methods and solutions to a real-world issue that has dominated headlines recently.